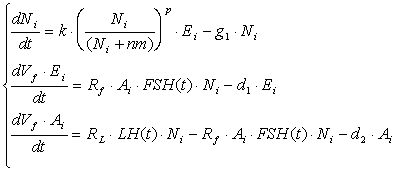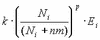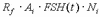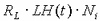Математические модели гормональной регуляции фолликулогенеза и возможности их использования
|
В настоящее время в большинстве центров, имеющих опыт работы по программам ЭКО, частота наступления беременности (ЧНБ) на перенос эмбриона достигает 20–30%, что практически не отличается от ЧНБ у здоровой пары в одном менструальном цикле [7]. Однако если наступление беременности для здоровой супружеской пары является вопросом времени, то в программе ЭКО каждая последующая попытка сопряжена с материальными и моральными потерями. Поэтому вопрос дальнейшего повышения эффективности указанного метода остается актуальным.
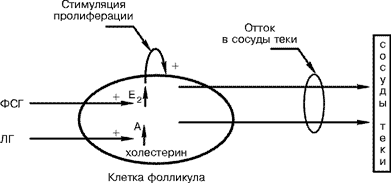
Хорошо известно, что успех исхода ЭКО во многом определяется результатом проведения индукции суперовуляции, целью которой является получение как можно большего количества зрелых, то есть способных к оплодотворению яйцеклеток. Как свидетельствуют многие авторы, при индукции суперовуляции с помощью кломифенцитрата в сочетании с менопаузальными гонадотропинами даже при оптимальном ответе яичников доля полученных при пункции незрелых ооцитов достигает 30% и более [7]. В ряде работ показано, что использование агонистов гонадотропин-рилизинг гормона (а-ГнРГ) позволяет снизить число незрелых яйцеклеток в 2 раза [7]. Таким образом, выбор схемы стимуляции может оказывать существенное влияние на результаты индукции суперовуляции, и постановка задачи оптимизации этой процедуры может иметь смысл. Наиболее существенными факторами, приводящими к формированию аномальной яйцеклетки, являются преждевременный (до наступления преовуляторного периода) выброс эндогенного ЛГ, а также высокий базальный уровень ЛГ [1, 5, 7]. По мнению большинства специалистов, констатация факта преждевременного выброса ЛГ является показанием к прекращению цикла стимуляции ввиду малой перспективности его удачного исхода. Отмечено, что преждевременный эндогенный пик ЛГ имеет место более чем в 10–15% случаев овариальной стимуляции кломифенцитратом и менопаузальными гонадотропинами [7], в то время как при использовании чМГ или чистых препаратов ФСГ спонтанный выброс ЛГ обычно отсутствует [16]. При состояниях, связанных с высоким базальным уровнем ЛГ, повышенным отношением ЛГ/ФСГ (более 2,5), а также в случае, когда в предыдущих циклах у пациенток наблюдалась мультифолликулярная реакция при назначении чМГ, для индукции суперовуляции показано применение чистых препаратов ФСГ [2]. Приведенные выше данные также подтверждают возможность и необходимость разработки методов оптимизации процедуры индукции суперовуляции с учетом индивидуальных характеристик женщины. Использование экзогенных гормональных препаратов при стимуляции яичников приводит к нарушению естественных гомеостатических механизмов регуляции роста и созревания фолликулов, поэтому задача управления системой гипофиз–яичники в циклах ЭКО целиком возлагается на врача, и результат стимуляции во многом зависит от выбора тактики ее ведения. Все решения о коррекции вида и дозы индукторов суперовуляции, времени введения тех или иных гормональных препаратов, а также их отмене и прекращении попытки ЭКО в данном менструальном цикле принимаются после оценки динамики ответа яичников на основании данных ультразвукового и гормонального мониторинга, полученных в процессе стимуляции. При любом методе стимуляции суперовуляции с помощью использования ультразвуковой диагностики постоянно контролируются число фолликулов, темпы их роста и величина фолликулов [9]. О полноценности развития фолликулов судят по данным как ультразвукового контроля динамики роста фолликулов [5], так и гормонального мониторинга изменений концентрации эстрадиола (Е2) в сыворотке крови [1]. Считается, что динамика уровня сывороточного Е2 лучше всего отражает как степень зрелости преовуляторных фолликулов, так и адекватность индукции суперовуляции [1]. Однако частота проведения гормональных исследований ограничена их высокой стоимостью. Использование же одного ультразвукового мониторинга для оценки ответа яичников на стимуляцию является недостаточно информативным [16]. Кроме того, в литературе нет единства взглядов относительно четких критериев, которыми можно было бы руководствоваться при интерпретации результатов мониторинга [1, 6, 7, 16]. В ситуациях, когда информация, полученная о физиологических процессах с помощью прямых методов, неполна, а отдельные характеристики труднодоступны для измерения, представляется перспективным использование косвенных методов оценки состояния исследуемой системы, к которым, в частности, относится математическое моделирование. Этот метод предусматривает замену исследований реального объекта исследованиями его математической модели, которая представляет собой уравнение или систему уравнений, описывающую взаимосвязь основных переменных, характеризующих реальный физиологический процесс или систему. Модель, адекватно описывающая процессы, происходящие в реальной системе, позволяет исследовать возможные ответы системы на внешние воздействия (например, введение гормональных препаратов, лекарственных веществ и т.д.) и может быть использована для анализа и интерпретации результатов клинических исследований и принятия оптимального решения об управлении реальной системой. Коротко рассмотрим задачи, которые должен решать врач на этапе индукции суперовуляции, и возможности их оптимизации с помощью методов математического моделирования. Важными моментами индукции суперовуляции являются определение типа реагирования пациентки на стимуляцию и прогнозирование исхода ЭКО. Применение индукции суперовуляции у клинически здоровых женщин с нормальным менструальным циклом выявило разные типы реакций яичников на стимуляцию [15, 16]. На основании показателей уровня Е2 в процессе индукции суперовуляции выделяют три вида реагирования – нормальный (концентрация сывороточного Е2 к моменту введения ХГ составляет 900–2000 пг/мл), слабый (ниже 900 пг/мл) и чрезмерный (более 2000 пг/мл) [1]. Группы пациенток со слабым и чрезмерным типами реагирования являются прогностически неблагоприятными в отношении наступления беременности. В первом случае существует высокий риск развития синдрома гиперстимуляции яичников, во втором – ответ яичников характеризуется как “плохой” и требует прекращения процедуры [1]. В обоих случаях для достижения успешного исхода ЭКО требуется подбор индивидуальной схемы стимуляции [16]. Как уже было сказано, в настоящее время оценка ответа яичников на гормональную стимуляцию и получение прогноза исхода и осложнений ЭКО основывается на данных ультразвукового и гормонального мониторинга. Вопрос о выборе схемы индукции суперовуляции решается до начала лечения, однако ее «настройка» на конкретную пациентку осуществляется непосредственно в процессе стимуляции, и, в основном, базируется на личном опыте специалистов. Ценность адекватной математической модели состоит в том, что ее параметры можно настроить так, чтобы она воспроизводила данные лабораторных и инструментальных исследований конкретной женщины. Такая процедура также является косвенным методом оценки параметров функционального состояния системы гипофиз–яичники данной женщины. Можно надеяться, что с помощью индивидуальной модели подбор режима стимуляции для конкретной женщины и соответственно предварительный прогноз исхода ЭКО возможно будет осуществлять до начала лечения. Одним из важных условий, влияющих на исход ЭКО, является правильный выбор момента введения ХГ на завершающем этапе индукции суперовуляции [1, 6, 7, 16]. Решение о моменте введения ХГ принимается на основании оценки функциональной зрелости фолликулов. Однако до настоящего времени в литературе нет единства взглядов относительно четких критериев выявления этого состояния. Одни авторы предлагают использовать значения Е2, полученные путем деления показателей сывороточного Е2 на число фолликулов, средний диаметр которых равен или превышает 15 мм [1], другие считают показанием к назначению ХГ достижение лидирующим фолликулом среднего диаметра 19 мм или 2–3 фолликулами – 17–18 мм [6] и т.д. Использование математической модели для решения этой задачи может быть эффективным в выборе как наиболее оптимального критерия для оценки зрелости преовуляторных фолликулов, так и возможного упрощения схемы мониторинга. Расчет с помощью модели момента времени, к которому растущие фолликулы достигнут функциональной зрелости, может помочь в определении момента начала мониторинга и момента введения ХГ. В настоящей работе дается обзор предложенных разными авторами математических моделей гормональной регуляции фолликулогенеза и обсуждаются перспективы применения методов математического моделирования для оптимизации индукции суперовуляции. Исторически интерес к использованию математических моделей в области гормональной регуляции репродуктивной функции женщин стимулировался необходимостью объяснить механизмы, исследование которых прямыми методами ограничено, во-первых, сложностью изучаемых явлений, что не позволяет системно проверить непротиворечивость выдвигаемых гипотез, во-вторых, морально-этическими соображениями. Ранние математические модели гипоталамогипофизарно-яичниковой системы посвящены исследованию возможных причин и механизмов, определяющих цикличность в гипоталамо-гипофизарно-яичниковой системе. В 1940 г. H.Lamport [17] с помощью математического моделирования пытался получить ответ на вопрос, может ли цикличность в системе гипофиз–яичники объясняться только функционированием отрицательной обратной связи между гипофизом и яичниками, когда “эффективные” концентрации гонадотропинов стимулируют продукцию эстрогенов, а последние, в свою очередь, снижают секрецию гонадотропинов. Если ответ на этот вопрос положителен, то математическая модель, построенная на этих предположениях, должна вести себя как автоколебательная система (подобная часам или генератору электрических колебаний), в которой генерируются незатухающие периодические колебания. Модель Lamport представляет собой систему двух дифференциальных уравнений первого порядка, которые описывают материальный баланс эстрогенов и ФСГ в плазме крови, причем действие эстрогенов формально моделируется как процесс выведения ФСГ из крови, скорость которого пропорциональна концентрации эстрогенов. Исследование поведения данной модели показало, что в такой системе возможны только затухающие периодические колебания уровня Е2. Таким образом, модель не давала удовлетворительного описания процессов гормональной регуляции менструального цикла женщины, что указывает на недостаточность заложенных в модель представлений. Следующей серьезной попыткой на пути создания адекватной модели менструального цикла у женщин была работа H.Thompson и соавт. [24]. В этой работе модель Lamport была дополнена следующим образом: скорость секреции Е2 предполагается пропорциональной не концентрации ФСГ, а размеру растущего фолликула. ФСГ, в свою очередь, управляет ростом фолликула (скорость роста фолликула пропорциональна концентрации ФСГ). При достижении заранее заданного размера фолликул овулирует (в модели его размер мгновенно снижается до нуля), и фолликулярная фаза завершается резким спадом эстрогенов. Таким образом, именно рост, а затем овуляция фолликула, продуцирующего Е2, предполагается определяющим фактором в возникновении периодичности системы. Модель состоит из трех дифференциальных уравнений, два из них, как и в модели Lamport, описывают материальный баланс эстрогенов и ФСГ в плазме крови, а третье – рост и овуляцию эстрадиолскретирующего фолликула. С помощью данной модели авторам удалось формально воспроизвести периодические незатухающие колебания сывороточных концентраций гормонов (ФСГ и Е2) в течение менструального цикла, которые генерируются в модели даже при постоянной концентрации ФСГ в крови (при отсутствии отрицательной обратной связи). В модели не учитывается влияние ЛГ на фолликулогенез, не рассматривается рост остальных гонадотропинзависимых фолликулов когорты, способных подвергаться атрезии и участвующих в формировании сывороточного Е2 и регуляции секреции ФСГ до момента селекции доминантного фолликула, поэтому использование ее в практических целях требует включения дополнительных предположений. Кроме того, в модели постулируются плохо объяснимые с физиологической точки зрения процессы. Так, ингибирование секреции ФСГ эстрогенами моделируется формально с помощью процесса выведения ФСГ из крови, скорость которого пропорциональна концентрации эстрогенов, что заведомо неверно, так как такой процесс будет происходить в модели даже при отсутствии в крови ФСГ. В уравнении, определяющем рост фолликула, не учитываются пролиферация и гибель клеток гранулезы. В работах С.П. Олимпиевой и соавт. была создана модель, в которой указанные выше противоречия были устранены [3, 4, 8]. Модель использовалась при создании компьютерной консультативной системы для осуществления интеллектуальной поддержки интерпретации результатов гормональных измерений при диагностике эндокринно-обусловленных нарушений женской репродуктивной функции. Показано, что модель воспроизводит многие наблюдающиеся в клинике патологические состояния в системе гипофиз–яичники, такие, как дисгенезия гонад, гиперпролактинемия, гипогонадотропный гипогонадизм, увеличение длительности фолликулярной фазы цикла на фоне увеличения массы жировой ткани и т.п. С помощью модели удалось установить соответствие между картиной зависимости от времени концентраций Е2, ФСГ и размера доминантного фолликула, с одной стороны, и вида нарушений в системе гипофиз–яичники и возможными экстраовариальными причинами этих нарушений, с другой. Разработанная модель и экспертная система могут быть использованы для выявления эндокринно-обусловленных нарушений репродуктивной функции на этапе обследования пациенток до начала лечения бесплодия методом ЭКО. Для использования при оптимизации режимов индукции суперовуляции модель необходимо дополнить так, чтобы учесть механизмы взаимодействия в когорте растущих фолликулов, влияние ЛГ на развитие фолликула и включить в нее более точное описание механизма регуляции продукции фолликулом андрогенов и эстрогенов. В 1972 г. R.Bogumil и соавт. представили эвристическую модель из 34 нелинейных уравнений (дифференциальных и алгебраических), которые описывали количественные и качественные изменения морфологии яичников и содержания гормонов в плазме и в фолликулярной жидкости в течение менструального цикла женщины [11, 12]. Авторы объединили в единую систему все существующие на тот момент знания о физиологии репродуктивной системы. В модели учитываются такие процессы, как регуляция эстрадиолом и прогестероном по принципу отрицательной обратной связи секреции ФСГ и «тонической» секреции ЛГ; овуляторный выброс по принципу «все или ничего» накопленного в клетках гипофиза ЛГ; рост преантральных и антральных фолликулов представлен увеличением массы клеток с учетом влияния Е2, андрогенов, ФСГ и ЛГ; образование антрума и накопление антральной жидкости; закономерности роста доминантного фолликула и его овуляции. С помощью уравнения баланса количества вступающих в рост и атрезирующих фолликулов (с учетом влияния ФСГ) определяется число «активных» в данный момент фолликулов. Учитываются закономерности лютеинизации фолликулов (в том числе и преждевременной); образования желтого тела цикла и желтого тела беременности; влияния гонадотропинов на синтез и секрецию стероидных гормонов яичниками. Модель Bogumil содержит очень большое количество индивидуальных параметров, вследствие чего она сложна для практического использования в клинике. С помощью численных экспериментов с моделью авторы продемонстрировали, что даже в условиях нормального функционального состояния системы «гипоталамус–гипофиз–яичники» незначительные и кратковременные однократные возмущения секреции гонадотропинов могут вызвать значительные вариации длительности менструального цикла вплоть до появления ановуляторных циклов. Данную модель, по-видимому, можно использовать для построения компьютерной обучающей системы по физиологии менструального цикла. Следующим этапом на пути построения моделей женской репродуктивной системы были работы H.Lacker [18] и Е.Akin и H.Lacker[10, 18–20]. Цель настоящей работы – изучение возможных механизмов формирования овуляторной квоты, или селекции фолликулов. Существует гипотеза, которая объясняет регуляцию количества овулирующих фолликулов локальными механизмами, действующими в пределах яичников. Однако эта гипотеза не согласуется с известным фактом, что при удалении одного яичника размер овуляторной квоты не меняется [21], а также противоречит статистическим закономерностям возникновения овулирующего фолликула в правом или левом яичнике. В модели рассматривается альтернативная гипотеза взаимодействия фолликулов через сывороточные концентрации гормонов – эстрадиола и гонадотропинов. Фолликулы секретируют эстрогены, которые управляют синтезом тропных гормонов гипофиза, а ФСГ и ЛГ, в свою очередь, регулируют созревание самих фолликулов. В основе критерия зрелости каждого фолликула принята скорость секреции Е2. Ответ фолликула (имеется в виду синтез Е2) на циркулирующие концентрации ФСГ и ЛГ зависит от степени его зрелости. Авторы постулируют существование единого для всех фолликулов закона роста, который в неявном виде отражает внутрисистемные механизмы, с помощью которых ФСГ и ЛГ регулируют скорость созревания фолликулов. Эта функция задает зависимость скорости роста фолликулов (в пересчете на одну эстрадиолсекретирующую клетку) от концентрации Е2 в крови и «зрелости» этого фолликула, определяемой по вкладу данного фолликула в сывороточную концентрацию Е2. Результаты численных экспериментов с моделью показывают, что в популяции растущих фолликулов с начальной зрелостью каждого, выбранной случайным образом, одни фолликулы овулируют, другие подвергаются атрезии. Изменение параметров “закона роста” фолликулов может привести к изменению наиболее вероятного числа овулирующих фолликулов, что позволяет с единых позиций объяснить существование как множественной, так и моноовуляции. Было показано, что размер популяции взаимодействующих фолликулов не влияет на наиболее вероятное число овулирующих фолликулов (что хорошо согласуется с данными A.Lipschutz [21]), но меняет форму частотного распределения числа овулирующих фолликулов при случайном распределении начальных зрелостей фолликулов, составляющих когорту. Было показано, что при некоторых значениях параметров “закона роста” фолликулов в системе возможно существование ановуляторных состояний. Предложенная теория регуляции развития фолликулов и формирования овуляторной квоты послужила толчком для ряда экспериментальных работ. Концепцию угнетения доминантным фолликулом роста остальных фолликулов когорты через циркулирующий Е2 проверяли на приматах, где этот эффект воспроизводился введением экзогенного Е2 с разной интенсивностью, продолжительностью и частотой [23, 25]. Результаты исследований показали, что экзогенный Е2 может вызывать атрезию фолликулов когорты, и в том числе доминантного, что послужило доказательством правильности предположений, заложенных в модели Lacker. Данную модель трудно использовать для оптимизации индивидуального режима стимуляции, поскольку при попытке настроить данную модель на клинические характеристики конкретной женщины возникают сложности определения параметров “закона роста”, так как в условиях in vivo практически невозможно измерить скорости секреции Е2 каждым фолликулом растущей когорты. Кроме того, в модели отсутствуют в явном виде концентрации гонадотропинов, управляющие ростом и созреванием фолликулов, что затрудняет ее использование в клинических целях. В предлагаемой авторами настоящей работы модели механизмы влияния гонадотропинов на скорость секреции Е2 отдельно взятым фолликулом учитываются в явном виде. Тропное действие гормонов гипофиза реализуется через регуляцию численности и функциональной активности популяции клеток гранулезы – основных эстрадиолсекретирующих клеток фолликула. При построении модели были сделаны следующие предположения. Под влиянием ЛГ клетки фолликула секретируют андростендион (А), который, в свою очередь, является субстратом для синтеза Е2. Синтез Е2 регулируется ФСГ. Е2 принимается в качестве основного фактора, непосредственно стимулирующего пролиферацию клеток. Скорость оттока гормонов из фолликула в сосуды теки пропорциональна их концентрации в фолликулярной жидкости. Влияние гонадотропинов на систему “фолликул” рассматривается как внешнее по отношению к данной системе (см. рисунок).
Математически модель роста отдельно взятого (i-го) фолликула представлена в виде дифференциальных уравнений материального баланса всех гормонов фолликулярной жидкости и клеток гранулезы в фолликуле:
где t – время; Ni – число клеток гранулезы i-го фолликула; Аi , Еi – концентрации андростендиона и эстрадиола в фолликулярной жидкости; FSH(t), LH(t) – задаваемые функции времени, которые описывают изменение уровня ФСГ и ЛГ в плазме крови; d1, d2 – константы скорости выведения из фолликулярной жидкости эстрогенов и андрогенов соответственно; g1 – константа скорости гибели клеток; Vf – объем фолликулярной жидкости; Rf , RL – коэффициенты чувствительности ферментативных систем фолликула к действию ФСГ и ЛГ соответственно; nm – константа, которая описывает зависимость скорости пролиферации от размера популяции клеток; k – константа скорости пролиферации клеток. Рассмотрим более подробно каждое уравнение. В первом уравнении рост фолликула описан через изменения размера популяции клеток гранулезы N(t) как функции времени. Скорость роста представляет разницу между скоростью пролиферации и скоростью гибели клеток.
а) зависимость удельной скорости пролиферации (на одну клетку) от числа клеток гранулезы в фолликулах разного диаметра, полученную при постоянных значениях ФСГ и ЛГ в культуре клеток гранулезы in vitro [13, 14]; б) зависимость числа клеток гранулезы в здоровом фолликуле от времени менструального цикла, оцененную по данным A.Gougeon [14]. Оказалось, что наиболее оптимальным показателем степени данной функции является p=2. Второе и третье уравнения описывают динамику концентраций эстрогенов и андрогенов в фолликулярной жидкости объемом Vf, где
Набор всех вышеперечисленных коэффициентов характеризует функциональное состояние данного фолликула, т.е. его способность реагировать определенным образом на внешнюю стимуляцию гонадотропинами. Оценка параметров модели проводилась по данным измерений морфометрических характеристик (время удвоения клеток гранулезы) здоровых антральных фолликулов от 2 мм в диаметре в условиях in vivo и in vitro [13, 14]. Результаты качественного исследования поведения модели показали, что в каждый момент времени существует зависящее от концентрации гонадотропинов граничное критическое значение размеров фолликулов, разделяющее растущие и атрезирующие фолликулы. Фолликулы с диаметром меньше критического атрезируют, а с диаметром больше критического – растут. В зависимости от концентраций гонадотропинов критический размер фолликулов меняется: при высоких концентрациях гонадотропинов в позднюю лютеиновую и раннюю фолликулярную фазы цикла этот размер мал, и в когорту включается относительно большое число фолликулов. По мере снижения концентраций гонадотропинов критический размер растет, и для тех фолликулов, размеры которых оказываются меньше критического, процесс роста сменяется процессом атрезии. До овуляции «доживают» те фолликулы, которые в течение всей фолликулярной фазы «обгоняли» критический размер. Зная индивидуальные параметры модели и режим стимуляции (зависимость концентраций гонадотропинов в плазме от времени), можно для любого начального распределения размеров фолликулов в когорте рассчитать судьбу каждого из них и определить степень их зрелости к моменту овуляции. В численных экспериментах с моделью мы рассмотрели развитие нескольких фолликулов с разной степенью зрелости с момента их рекрутирования в позднюю лютеиновую фазу предшествующего менструального цикла и до периовуляторного периода. Сывороточные концентрации гонадотропинов задавались в соответствии с экспериментальными данными K.McNatty и соавт. [22]. Результаты численных экспериментов показывают, что модель воспроизводит известный факт о том, что доминантным становится наиболее зрелый фолликул, то есть тот, который к моменту снижения уровня ФСГ имел наибольший диаметр и высокий уровень секреции Е2. Предварительный анализ модели показывает, что подбор индивидуальных параметров модели можно производить, используя сывороточные концентрации Е2, ФСГ и ЛГ, а также измерения диаметра фолликулов по данным ультразвукового исследования. Все эти данные возможно получить методами гормонального и ультразвукового мониторинга, которые используются в программе ЭКО, и с их помощью можно попытаться настроить параметры модели на характеристики репродуктивной системы конкретной женщины. Если оценить параметры модели по данным конкретной пациентки до начала стимуляции, на модели можно “проиграть” использование различных схем и попробовать сделать прогноз исхода ЭКО и подбор таких концентраций гонадотропинов, которые позволят вырастить у данной женщины определенное число фолликулов с определенной степенью зрелости. Если данные получены во время стимуляции, а исход ЭКО был неудачен, можно надеяться, что модель будет полезна при подборе индивидуального режима следующей стимуляции. Настроенную на конкретную пациентку модель предполагается возможным использовать для прогнозирования момента времени, к которому растущие фолликулы в стимулированном цикле достигнут функциональной зрелости, что может помочь в определении момента как начала ультразвукового и гормонального мониторинга, так и введения ХГ. Все вышеперечисленное дает возможность надеяться, что развитие математического моделирования позволит включить его в арсенал методов, которые использует врач для оптимизации режимов стимуляции в программе ЭКО. М.П. Матвеева, В.В. Киликовский, С.П. Олимпиева Кафедра медицинской и биологической кибернетики Российского государственного медицинского университета, Москва Литература 1. Аншина М.Б. Принципы гормонального мониторинга в программе ЭКО. Пробл репрод 1995; 2: 43–48. 2. Боярский К.Ю. Овариальная стимуляция и фолликулогенез в конце 90-х годов: на пороге будущего. 1997; 4: 61–68. 3. Задорожная И.К. Экспертная система интерпретации результатов гормональных измерений у женщин с эндокринно обусловленными нарушениями репродуктивной функции. Дис. ... к.м.н. М 1994; 156–157. 4. Киликовский В.В., Олимпиева С.П., Задорожная И.К. Экспертная консультативно-диагностическая система по эндокринным нарушениям репродуктивной функции женщины (РЕПРОКОД). Информационные системы поддержки медицинского страхования. Респ. сб. науч. тр. под ред. проф. С.А. Гаспаряна. М 1994; 154–162. 5. Ковальский Г.Б., Китаев Э.М., Рыжавский Б.Я. и др. Структурные основы генеративной и эндокринной функции яичников в норме и патологии. Санкт-Петербург. 1996; 176–182. 6. Корсак В.С., Исакова Э.В., Каменецкий Б.А. и др. О критериях назначения хорионического гонадотропина при контролируемой индукции суперовуляции. Пробл репрод 1998; 3: 50–54. 7. Никитин А.И. Факторы неудач в программах вспомогательной репродукции. Пробл репрод 1995; 2: 36–42. 8. Олимпиева С.П., Киликовский В.В., Задорожная И.К. и др. Система интеллектуальной поддержки интерпретации результатов гормональных измерений при нарушениях женской репродуктивной функции. Труды III Международного форума “Стратегия здоровья: интеллектуальное обеспечение медицины”. Гурзуф, 14–20 мая, 1994; 70–71. 9. Сметник В.П., Тумилович Л.Г. Неоперативная гинекология. М 1997:476–480. 10. Akin E., Lacker H.M. Ovulation control: the right number or nothing. J Math Biol 1984; 20: 113–132. 11. Bogumil R.J., Ferin M., Rootenberg J. et. al. Mathematical studies of the human menstrual cycle. I. Formulation of a mathematical model. J Clin Endocrinol Metab 1972; 35: 126–142. 12. Bogumil R.J., Ferin M., Vande Wiele R.L. Mathematical studies of the human menstrual cycle. II.Simulation performance of a model of the human menstrual cycle. J Clin Endocrinol Metab 1972; 35: 144–156. 13. Gougeon A. Rate of follicular growth in the human ovary. In: Rolland R., van Hall E.V., Hiller S.G., McNatty K.P., Schoemaker J. (eds) Follicular Maturation and Ovulation. Exerpta Medica, Amsterdam, 1982; 155–163. 14. Gougeon A. Regulation of ovarian follicular development in primates: facts and hypotheses. Endocrin Rev 1996; 17: 121–155. 15. Hodgen G.D. Ovarian function for multiple follicle maturation. Clin Obstet Gynecol 1986; 29(1):127–140. 16. Kerin J.F., Warnes G.M. Monitoring of ovarian response to stimulation in vitro fertilisation cycles. Clin Obstet Gynecol 1986; 29: 158–206. 17. Lamport H. Periodic changes in blood estrogen. Endocrinol 1940; 27:673–679. 18. Lacker H.M. Regulation of ovulation number in mammals: a follicle interaction law that controls maturation. Biophys J 1981; 35: 433–454. 19. Lacker H.M., Beers W.H., Meuli L.E. et. al. A theory of follicular selection: I. Hypotheses and examples. Biol Reprod 1987; 37: 570–580. 20. Lacker H.M., Beers W.H., Meuli L.E. et. al. A theory of follicular selection: II. Computer simulation of estraiol administration in the primate. Biol Reprod 1987; 37: 581–588. 21. Lipschutz A. New developments in ovarian dynamics and the law of follicular constancy. Br J Exp Biol 1928; 5:283–91. 22. McNatty K.P., Hunter W.M., McNeilly A.S. et. al. Changes in the concentration of pituitary and steroid hormones in the follicular fluid of human graafian follicles throughout the menstrual cycle. J Endocrinol 1975; 64: 555–571. 23 Meuli L.E., Lacker H.M., Thau R.B. Experimental evidence supporting a mathematical theory of the physiological mechanism regulating follicle development and ovulation number. Biol Reprod 1987; 37: 589–594. 24. Thompson H.E., Horgan J.D., Delfs E. A simplified mathematical model and simulations of the hypophysis-ovarian endocrine control system. Biophys J 1969; 9: 278. 25. Zeleznik A.J., Kubik C.J. Ovarian responses in macaques to pulsatile infusion of follicle-stimulation hormone and luteinizing hormone: increased sensitivity of the maturating follicle to FSH. Endocrinology 1986; 119: 2025–2032. |